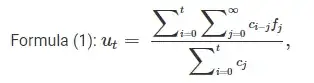The definition of mortality rate that you've given does not match any practical definition I'm familiar with.*
When people talk about the mortality rate of a disease, what they usually mean is the case fatality rate or the death-to-case ratio, which is simply defined as Nd / Ni, where Nd is the number of deaths attributed to the disease over a given time period and Ni is the total number of new cases of the disease observed during the same time period. By this definition, the current case fatality rate of 2019-nCov according to your quoted figures is 362 / 17491 ≈ 2.07%.
(The tracker seems to have been updated since you asked your question, and now lists a total of 20679 confirmed cases and 427 deaths, for a CFR of 427 / 20679 ≈ 2.06%.)
*) As a theoretical definition of the mortality rate in the long run, when all infected patients have either died or recovered, it can sort of make sense. But then it becomes equivalent to the usual definition of the case fatality rate.
To compare this with your definition of "mortality rate" (as Nd / (Nd + Nr), where Nr is the number of individuals who have recovered from the disease), we need to start by observing that there's no single universal and unambiguous definition of what "recovering from a disease" means. Commonly used definitions tend to be something like "no symptoms for X days" and/or "viral load below N particles per mL for X days" or simply "whenever a doctor declares that you're healthy again and lets you out of the hospital".
Now, let's say that we're using a (somewhat) objective definition of recovery like "no detectable symptoms for two days". The first observation is that any epidemic first observed less than two days ago would, according to your definition, inevitably have a mortality rate of 100% simply because none of the people infected so far would have had time to be considered definitely recovered yet. (That is assuming that at least one person had died from the infection; otherwise both the numerator and the denominator would be zero, and the rate thus undefined.)
Further, even after some of the earliest cases have been symptom-free long enough to be counted as recovered, your definition would still yield a highly upwards biased estimate of the "true" long-term fatality rate during the early phase of the epidemic, when the number of new cases per day is still increasing. This is because, for most infectious diseases, any deaths typically occur when the disease is at its most severe state, whereas those who survive the disease will then experience a gradual decline in symptoms as their immune system succeeds in halting and reversing the progress of the infection.
For an illustrative example, let's consider a hypothetical disease with a theoretical 1% long-term average CFR — that is to say, exactly 1% of all (recognizably) infected patients will die of the disease. Let's further assume that this disease typically takes two days to progress from the initial onset of recognizable symptoms to the state of maximum severity, which is when most of the deaths occur. After this, assuming that the patient survives, the symptoms gradually decline over the following three days. As remission is possible (but rare), doctors will generally consider a patient recovered only after showing no symptoms for at least two days. Thus, a typical case would progress as follows:
onset of symptoms → increasing symptoms (2 days) → peak severity → declining symptoms (3 days) → no symptoms → observation (2 days) → officially recovered (total time: approx. 7 days from onset)
or, for the 1% of patients for whom the disease is fatal:
onset of symptoms → increasing symptoms (2 days) → death (total time: approx. 2 days from onset)
Now, let's assume that, during the early period of an epidemic when the infection is still spreading exponentially, the number of new cases increases by a factor of 10 every three days. Thus, during this period, the number of new cases, recoveries and deaths per day might grow approximately as follows (assuming for the sake of the example that exactly 1%, rounded down, of the patients diagnosed on each day will die two days later):
| cases | recovered | deaths | | |
day | new | total | new | total | new | total | Nd / Ni | Nd/(Nd+Nr) |
----+-------+-------+-------+-------+-------+-------+---------+------------+
1 | 1 | 1 | 0 | 0 | 0 | 0 | 0.00% | N/A |
2 | 2 | 3 | 0 | 0 | 0 | 0 | 0.00% | N/A |
3 | 5 | 8 | 0 | 0 | 0 | 0 | 0.00% | N/A |
4 | 10 | 18 | 0 | 0 | 0 | 0 | 0.00% | N/A |
5 | 20 | 38 | 0 | 0 | 0 | 0 | 0.00% | N/A |
6 | 50 | 88 | 0 | 0 | 0 | 0 | 0.00% | N/A |
7 | 100 | 188 | 0 | 0 | 0 | 0 | 0.00% | N/A |
8 | 200 | 388 | 1 | 1 | 0 | 0 | 0.00% | 0.0% |
9 | 500 | 888 | 2 | 3 | 1 | 1 | 0.11% | 25.0% |
10 | 1000 | 1888 | 5 | 8 | 2 | 3 | 0.16% | 27.3% |
11 | 2000 | 3888 | 10 | 18 | 5 | 8 | 0.21% | 30.8% |
12 | 5000 | 8888 | 20 | 38 | 10 | 18 | 0.20% | 32.1% |
As you can see from the table above, naïvely calculating the case fatality rate as (total number of deaths) / (total number of cases) during this exponential growth period does underestimate the true long-term CFR by a factor of (in this case) about 5 due to the two-day lag time between infection and death. On the other hand, using your formula of (total deaths) / (total deaths + recovered) would overestimate the true CFR by a factor of about 30!
Meanwhile, let's assume that, after the first 12 days, the growth of the epidemic saturates at 10,000 new cases per day. Now the total numbers will look like this:
| cases | recovered | deaths | | |
day | new | total | new | total | new | total | Nd / Ni | Nd/(Nd+Nr) |
----+-------+-------+-------+-------+-------+-------+---------+------------+
13 | 10000 | 18888 | 50 | 88 | 20 | 38 | 0.20% | 30.2% |
14 | 10000 | 28888 | 99 | 187 | 50 | 88 | 0.30% | 32.0% |
15 | 10000 | 38888 | 198 | 385 | 100 | 188 | 0.48% | 32.8% |
16 | 10000 | 48888 | 495 | 880 | 100 | 288 | 0.59% | 24.7% |
17 | 10000 | 58888 | 990 | 1870 | 100 | 388 | 0.66% | 17.2% |
18 | 10000 | 68888 | 1980 | 3850 | 100 | 488 | 0.71% | 11.2% |
19 | 10000 | 78888 | 4950 | 8800 | 100 | 588 | 0.74% | 6.3% |
20 | 10000 | 88888 | 9900 | 18700 | 100 | 688 | 0.77% | 3.5% |
21 | 10000 | 98888 | 9900 | 28600 | 100 | 788 | 0.80% | 2.7% |
As you can see, the two measures of mortality rate do eventually start converging as the growth of the epidemic slows down. In fact, in the long run, as the majority of patients either recover or die, they do both end up converging to the "true" long-term case fatality rate of 1%. But by then, the epidemic will be basically over.
There are various ways to obtain a more accurate estimate of the long-term fatality rate even during the early exponential growth phase of an epidemic. One such method would be to look at the outcomes of a single cohort of patients diagnosed at the same time. For our hypothetical example epidemic, looking e.g. at just the 1000 patients diagnosed on day 10, we could get an accurate estimate of the CFR by day 12 simply by dividing the 10 deaths within that cohort by the total number of patients in the cohort. Furthermore, observing multiple cohorts would give us a pretty good idea of how long after diagnosis we would need to wait before the estimated case fatality rate for each cohort gets close to its final true value.
Unfortunately carrying out this kind of cohort analysis for 2019-nCov would require more detailed information than the tracker you've linked to provides. Even the time series spreadsheet the tracker links to doesn't directly provide such detailed cohort data, although it might be possible to obtain better estimates from it by making some more or less reasonable assumptions about the typical progress of the disease.
Addendum: A few preliminary cohort studies of the kind I describe above do appear to have already been published for 2019-nCoV.
In particular, "A novel coronavirus outbreak of global health concern" by Wang et al. and "Clinical features of patients infected with 2019 novel coronavirus in Wuhan, China" by Huang et al., both published on January 24 in The Lancet, note that, out of the first 41 patients diagnosed with 2019-nCoV before Jan 2, 2020 in Wuhan, six had died (and 28 had been discharged, leaving seven hospitalized) by Jan 22, giving a case fatality rate of 14.6% in this cohort.
However, they do advise treating this figure with due caution, noting a number of reasons (besides just the small number of cases examined) why it may not fully reflect the eventual long-term CFR:
"However, both of these [CFR] estimates [of 14.6% from the 41 patient cohort and of 2.9% from all 835 cases confirmed at the time of writing] should be treated with great caution because not all patients have concluded their illness (ie, recovered or died) and the true number of infections and full disease spectrum are unknown. Importantly, in emerging viral infection outbreaks the case-fatality ratio is often overestimated in the early stages because case detection is highly biased towards the more severe cases. As further data on the spectrum of mild or asymptomatic infection becomes available, one case of which was documented by Chan and colleagues, the case-fatality ratio is likely to decrease."
There's also a later paper titled "Epidemiological and clinical characteristics of 99 cases of 2019 novel coronavirus pneumonia in Wuhan, China: a descriptive study" by Chen et al., published on Jan 30, that examines a cohort of 99 patients diagnosed between Jan 1 to Jan 20 and reports a CFR of 11% within this cohort. However, the study only followed these patients up to Jan 25, by which time more than half of them (57 out of 99) still remained hospitalized.